二叉树

链表是一个只有一个next指针的数据结构，而二叉树是有2个，left，right的数据结构。二叉树的性质有很多，完全二叉树，二叉搜索树。
其中最重要的就是要掌握二叉树的遍历，前中后序深度优先递归遍历DFS和广度优先BFS迭代遍历。

快速查看遍历顺序： 画点法，在每个节点的 前中后画点，从左边画线，看经过的路径顺序
关键点

1. 在解题时，递归函数的返回值与如果操作返回值很关键，直接决定你能否得到正确答案。
2. 双层递归（下面例子）
3. 方向控制（下面有例子）

//前
func preorderTraversal(root: TreeNode?) {
    guard let root = root else { return }
    print(root.val)
    preorderTraversal(root: root.left)
    preorderTraversal(root: root.right)
}

preorderTraversal(root: treeNode3)

//中
func inorderTraversal(root: TreeNode?) {
    guard let root = root else { return }
    
    inorderTraversal(root: root.left)
    print(root.val)
    inorderTraversal(root: root.right)
}

inorderTraversal(root: treeNode3)

//hou
func postorderTraversal(root: TreeNode?) {
    guard let root = root else { return }
    
    postorderTraversal(root: root.left) //3 5 7
    postorderTraversal(root: root.right)
    
    print(root.val)
}

postorderTraversal(root: treeNode3)

//广度优先
//一层层的递进，每一次 while 都把这一层的 全走一遍
class Solution {
    func maxDepth(_ root: TreeNode?) -> Int {
        if root == nil {
            return 0
        }
        
        var queue: [TreeNode?] = []
        var deep: Int = 0
        
        queue.append(root)
        
        while !queue.isEmpty {
            //这一步是关键，保证每次是循环当前层的节点 这样才能计算出多少层
            //没有size> 0 的 while，其实也能遍历所有节点，但就无法计算多少层
            var size = queue.count
            while size > 0 {
                var node = queue.first!
                queue.removeFirst()
                
                if node?.left != nil {
                    queue.append(node!.left)
                }
                
                if node?.right != nil {
                    queue.append(node!.right)
                }
                
                size -= 1
            }
            
            deep += 1
        }
        
        return deep
    }
}

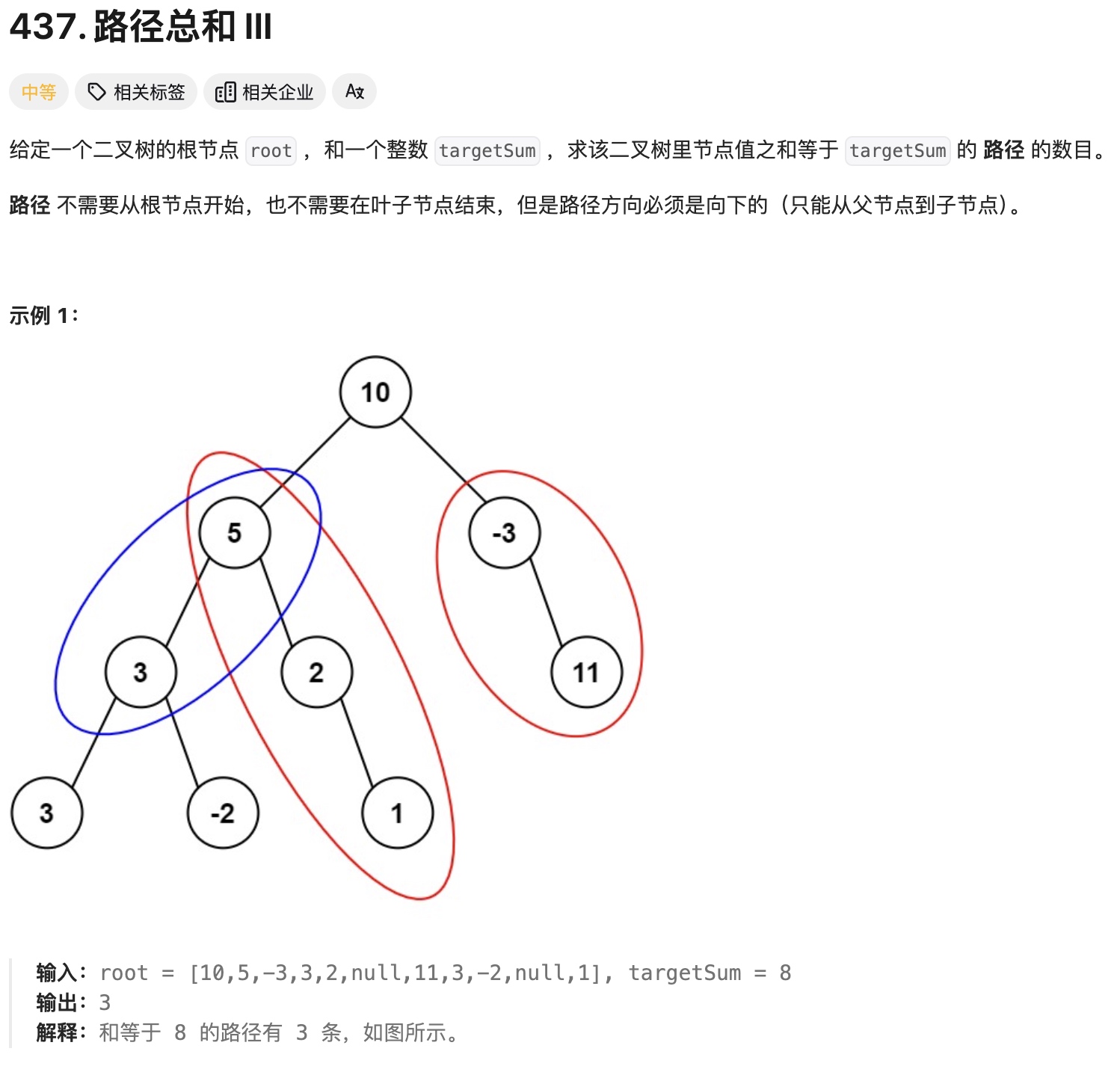
双层递归，从第一个节点开始递归遍历，然后从左，右，一直到最后

class Solution {
//    var sum = 0
//    var res = 0
    
    func pathSum(_ root: TreeNode?, _ targetSum: Int) -> Int {
        guard let root = root else { return 0 }
        
        var res = preorderTraversal(root: root, targetSum)
        res += pathSum(root.left, targetSum)
        res += pathSum(root.right, targetSum)
        return res
    }
    
    func preorderTraversal(root: TreeNode?, _ targetSum: Int) -> Int  {
        
        var res = 0
        
        guard let root = root else {
            return 0
        }
        
        if root.val == targetSum {
            res = 1
        }
        
        res += preorderTraversal(root: root.left, targetSum - root.val)
        res += preorderTraversal(root: root.right, targetSum - root.val)
        return res
    }
}

https://leetcode.cn/problems/longest-zigzag-path-in-a-binary-tree/description/?envType=study-plan-v2&envId=leetcode-75

这道题我开始是想双层递归的，但超时。这道题的关键是 如果在遍历的时候，“控制”方向，题目要求交错，那如果同向，那就要重新开始计算了，如果反向，就+1.

class Solution {

    var longestPath = 0

    func longestZigZag(_ root: TreeNode?) -> Int {
        guard let root = root else {
            return 0
        }

        preorderTraversal(root.left, currentLongth: 1, isLeft: true)
        preorderTraversal(root.right, currentLongth: 1, isLeft: false)
        return longestPath - 1
    }

    func preorderTraversal(_ root: TreeNode?, currentLongth: Int, isLeft: Bool) {
        guard let root = root else {
            return
        }
        print(root.val)
        var currentLongth = currentLongth
        currentLongth += 1
        longestPath = max(currentLongth, longestPath)

        preorderTraversal(root.left, currentLongth: isLeft ? 1 : currentLongth, isLeft: true)
        preorderTraversal(root.right, currentLongth: isLeft ? currentLongth : 1, isLeft: false)
    }
}

二叉树迭代方式遍历

//前序 注意是先右在左
func inorderTraversal(root: TreeNode?) -> [Int] {
    var result: [Int] = []
    var stack: [TreeNode] = []
    
    guard let root = root else { return result }
    
    stack.append(root)
    
    while !stack.isEmpty {
        let node = stack.removeLast()
        result.append(node.val)
        
        if let left = node.right {
            stack.append(left)
        }
        
        if let right = node.left {
            stack.append(right)
        }
    }
    
    return result
}

//后序
func postorderTraversal(root: TreeNode?) -> [Int] {
    var result: [Int] = []
    var stack: [TreeNode] = []
    
    guard let root = root else { return result }
    
    stack.append(root)
    
    while !stack.isEmpty {
        let node = stack.removeLast()
        result.append(node.val)
        
        if let right = node.left {
            stack.append(right)
        }
        
        if let left = node.right {
            stack.append(left)
        }
    }
    
    //先序遍历是 中左右，在代码实现的时候 我们是先右入栈在左入栈，因为栈是先进后出
    //我们改成 中 左 右，然后在将数组倒序
    //后序是 左右中，
    
    return result.reversed()
}

//中序
//有一说一 没太理解
//但可以先记为： 双while，内部while 一直向左边找，入栈
//到最深后 出栈，然后cur = cur.right
func inorderTraversal(_ root: TreeNode?) -> [Int] {
    var result: [Int] = []
    var stack: [TreeNode] = []
    var cur: TreeNode? = root
    
    while cur != nil || !stack.isEmpty {
        while cur != nil {
            stack.append(cur!)
            cur = cur?.left
        }
        
        let node =  stack.removeLast()
        result.append(node.val)
        cur = node.right
    }
    
    return result
}